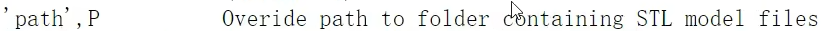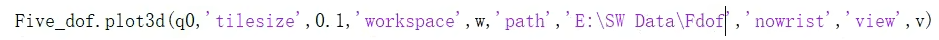[TOC]
“在你的专业领域里,你要像一个坚韧的农夫一样,一遍又一遍,向深处耕耘”
已购课程:
【史上最强机械臂教程】机械臂运动学、轨迹规划和动力学控制仿真-AC今夜有雨 (付费课程)语雀 https://www.yuque.com/dashboard/books#collab
Matlab机器人工具箱入门指南 • 汪迪 https://class.guyuehome.com/p/t_pc/course_pc_detail/column/p_615fb0e4e4b0dfaf7faa9725
学习计划 1.数理基础和编程:
线性代数:极其重要,是理解和表示向量、空间变换、矩阵运算等的基础。
Python:具身智能研究和开发中最主流的编程语言,拥有丰富的库和社区支持。
Matlab机器人工具箱: 主要用于验证机械臂的算法,对于从零开始学习机器人的运动学和动力学小白来说极易上手,里面有基本的机器人运动学和动力学函数,可通过查看底层函数,加强理论知识的学习,还可以在此基础上快速开发自己的算法。
ROS+Moveit+OMPL:OMPL集成了最先进的运动规划、操作、3D感知、运动学、控制与导航算法。再结合Rviz和Gazebo等工具,就十分完美了。
2.机器人理论:
目标:扎扎实实打好空间变换、DH建模、正逆运动学、轨迹规划、雅可比矩阵等动力学 (补理论力学) 的基础。
行动:重新过一遍理论知识,用一个专门的本子做笔记、推导,对于逆运动学要自己手算一遍,不能只会调库。
1)齐次变换:用一个4x4的齐次变换矩阵来描述两个坐标系之间的关系,
熟悉坐标表示方式:坐标系{B}在{A}下的位姿如何表示。
左乘和右乘的区别。
了解旋转矩阵每一列的含义,学会如何通过目测写出两个坐标系之间的旋转矩阵。
姿态的表示方式:RPY角,各种欧拉角、轴角表示。
2)运动学:
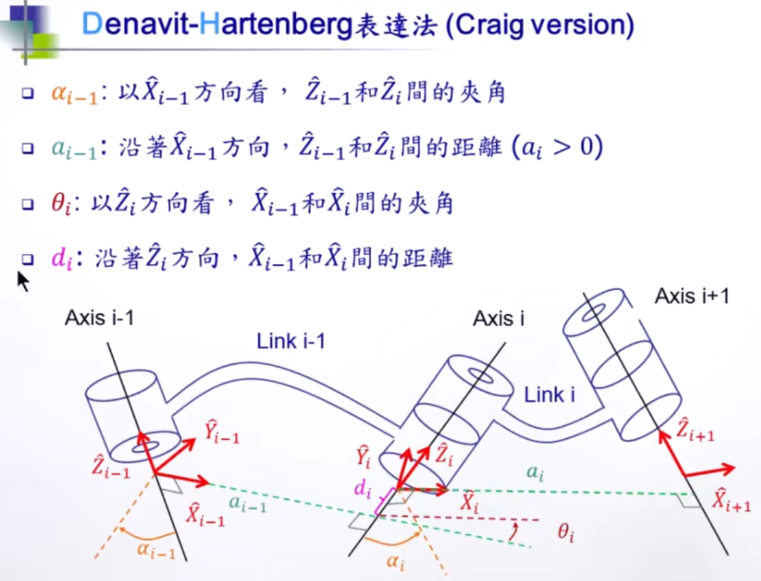
为了方便计算两个连杆之间的相对位姿,需要学习DH建模方法
建立坐标系
计算DH参数
计算变换矩阵
正解:知道每个连杆两两之间的坐标变换,就可以通过矩阵乘法计算出最后的末端位姿了。
逆解:闭式解法(解析)、数值解法(如Jacobian迭代)。通过不断调整上面几个矩阵的位置,尝试找到可以单独求解的未知数即可。虽然有些繁琐,但是对于初学者来说一定要亲手推一推六轴机械臂的运动学逆解公式,并编程实现。 重点是解析解(特殊构型的封闭解析解,解析解需要满足Pieper准则,否则只能用数值解)
3)轨迹规划:
用MATLAB实现直线,圆弧,梯形,三次五次多项式,SLERP,SQUAD,NURBS。
任务空间(笛卡尔空间)控制更贴近目标
4)雅可比计算:
线速度/角速度与关节速度之间的映射关系
用于控制与奇异性分析
5)动力学建模:
Lagrangian(拉格朗日)法:基于能量
Newton-Euler法:基于力和加速度
获取运动方程:M(q)q¨+C(q,q˙)q˙+G(q)=τM(q)\ddot{q} + C(q,\dot{q})\dot{q} + G(q) = \tau
了解阻抗控制、导纳控制、参数辨识
学习资源 了解一个领域的常见技巧
谷歌学术搜关键词:找到survey,或者引用数比较高的论文,然后用ChatPaper总结,或者学术版GPT免费翻译,快速阅读。
如果是最新的论文:Arxiv搜关键词。
看paperwithcode的排行榜,比如:https://paperswithcode.com/sota
如果是代码复现,可以Github搜:awesome+xxx ,一般会有大佬给你整理好相关的资料。
专栏 Robotics https://blog.csdn.net/jldemanman/category_7433626.html
机械臂速成小指南 https://blog.csdn.net/m0_53966219/category_11761138.html
【Matlab 六自由度机器人】系列文章汇总https://blog.csdn.net/AlbertDS/article/details/123968265?spm=1001.2014.3001.5501**(写的很细致,强推) **
https://blog.csdn.net/vittore_li/category_11556951.html?spm=1001.2014.3001.5482
机器人进阶之路 https://www.zhihu.com/column/c_1241771327444774912
机器人技术基础之运动学 https://www.zhihu.com/column/c_1693921850789429248?utm_campaign=&utm_medium=social&utm_psn=1896366318900467549&utm_source=qq
【史上最强机械臂教程】机械臂运动学、轨迹规划和动力学控制仿真-AC今夜有雨 语雀 https://www.yuque.com/dashboard/books#collab
深蓝学院:机器人人抓取与操作 https://www.shenlanxueyuan.com/course/774
具身智能技术指南 Embodied-AI-Guide https://github.com/TianxingChen/Embodied-AI-Guide?tab=readme-ov-file#vla
全网最全具身智能知识库 https://yv6uc1awtjc.feishu.cn/wiki/WPTzw9ON0ivIVrkLjVocNZh8nLf
具身智能入门指南 https://lcn9rz94g08a.feishu.cn/wiki/LhqzwYwcdiuyWvkdmgdc0OQ2nOc
国内首个具身智能算法与实战全栈教程(已购买)https://gkklv.duanshu.com/?#/
具身智能之心知识星球
关于机械臂操纵(抓取、操纵)方向的论文仓库:https://github.com/BaiShuanghao/Awesome-Robotics-Manipulation
MATLAB机器人工具箱 【MATLAB教程_台大郭彦甫(14课)原视频补档】 https://www.bilibili.com/video/BV1GJ41137UH/?share_source=copy_web&vd_source=4eaa4760820b4cda603e510d556578ac
机器人工具箱笔记https://www.yuque.com/office/yuque/0/2022/doc/27569122/1667006650805-39b5fcad-561e-4dc6-bd08-305d0d51b78d.doc?from=https%3A%2F%2Fwww.yuque.com%2Fjinyeyouyu-v4bnu%2Fwbelr0%2Fcs36y2
Matlab机器人工具箱入门指南 • 汪迪 https://class.guyuehome.com/p/t_pc/course_pc_detail/column/p_615fb0e4e4b0dfaf7faa9725
【MATLAB机器人工具箱10.4 机械臂仿真教学(未完结)】 https://www.bilibili.com/video/BV1q44y1x7WC/?share_source=copy_web&vd_source=4eaa4760820b4cda603e510d556578ac
【MATLAB教程_台大郭彦甫(14课)原视频补档】 https://www.bilibili.com/video/BV1GJ41137UH/?share_source=copy_web&vd_source=4eaa4760820b4cda603e510d556578ac
空间描述和变换 具身智能知识库-坐标系与位姿变换https://yv6uc1awtjc.feishu.cn/wiki/CIuTwmBOoip1cQk31wgc81Tanvd
DH建模 PPT-https://wenku.baidu.com/view/001c588602d8ce2f0066f5335a8102d277a26148.html?_wkts_=1746360331828
详细介绍如何使用MATLAB中的机器人工具箱建立机器人模型(DH法建模)(三自由度机械臂)https://blog.csdn.net/qq_44339029/article/details/109708454?ops_request_misc=&request_id=&biz_id=102&utm_term=%E6%9C%BA%E6%A2%B0%E8%87%82dh&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduweb~default-1-109708454.142
工业六轴机器人常见的MOD(改进)-DH模型建立方法-https://blog.csdn.net/Vittore_Li/article/details/122219529?spm=1001.2014.3001.5502
正逆运动学 如果是自己设计机械臂或者机械臂末端,需要自己推导运动学公式,若是购买的机械臂成品,则可直接调用机械臂厂家提供的API。
想要快速了解什么是IK,FK的同学可以看这个,可以建立一个粗略的认知:https://www.bilibili.com/video/BV18E411v7F9/?spm_id_from=333.337.search-card.all.click&vd_source=b14220472557bfa1918f3d0faa38bdc1
较为简单的过一遍IK和FK的原理可以看这个:
https://blog.csdn.net/Dwzsa/article/details/142386529?spm=1001.2101.3001.6650.3&utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7ECTRLIST%7ECtr-3-142386529-blog-109314877.235%5Ev43%5Epc_blog_bottom_relevance_base7&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7ECTRLIST%7ECtr-3-142386529-blog-109314877.235%5Ev43%5Epc_blog_bottom_relevance_base7&utm_relevant_index=6
puma560运动学 https://blog.csdn.net/howard789/category_11645542.html?fromshare=blogcolumn&sharetype=blogcolumn&sharerId=11645542&sharerefer=PC&sharesource=qq_52769953&sharefrom=from_link
3、4自由度机械臂正逆解推导与代码实现 • 吴健新 https://class.guyuehome.com/p/t_pc/course_pc_detail/column/p_61839a62e4b0ac1ecd65bf47
正运动学
手推正运动学-https://blog.csdn.net/AlbertDS/article/details/110631364
puma560 手推正运动学https://blog.csdn.net/howard789/article/details/123142492?fromshare=blogdetail&sharetype=blogdetail&sharerId=123142492&sharerefer=PC&sharesource=qq_52769953&sharefrom=from_link
较为详细的视频课(南科大贾振中):
FK1 https://www.bilibili.com/video/BV1Ve4y127Uf/?spm_id_from=333.788.recommend_more_video.0&vd_source=b14220472557bfa1918f3d0faa38bdc1
FK2 https://www.bilibili.com/video/BV1a14y157uL/?spm_id_from=333.788.videopod.sections&vd_source=b14220472557bfa1918f3d0faa38bdc1
逆运动学
求解方法:数值解和解析解
手推逆运动学-https://blog.csdn.net/AlbertDS/article/details/123679114
手推puma 560 逆运动学https://blog.csdn.net/howard789/article/details/123150942?fromshare=blogdetail&sharetype=blogdetail&sharerId=123150942&sharerefer=PC&sharesource=qq_52769953&sharefrom=from_link
MATLAB机器人工具箱中机器人逆解是如何求出来的?https://www.zhihu.com/question/41673569/answer/129670927?share_code=IhuO3vQR063S&utm_psn=1907032115301823715
【一起用Matlab从零手写六轴机械臂正逆解和轨迹规划】 https://www.bilibili.com/video/BV1UY411N7Xr/?share_source=copy_web&vd_source=4eaa4760820b4cda603e510d556578ac (不调用机器人工具箱)
机器人厂商的逆解是怎么做的 https://www.zhihu.com/question/380943528/answer/1095992504?share_code=10Gaq9dtXhHIi&utm_psn=1907032724964882059
较为详细的视频课(南科大贾振中):
IK1 https://www.bilibili.com/video/BV1PD4y1t7xP/?spm_id_from=333.337.search-card.all.click&vd_source=b14220472557bfa1918f3d0faa38bdc1
IK2 https://www.bilibili.com/video/BV1Tt4y1T79Z/?spm_id_from=333.788.recommend_more_video.0&vd_source=b14220472557bfa1918f3d0faa38bdc1
Book:
较为详细的IK理论 https://motion.cs.illinois.edu/RoboticSystems/InverseKinematics.html
轨迹规划 具身智能知识库-机器人轨迹规划https://yv6uc1awtjc.feishu.cn/wiki/Zmk2we1JQiv9gBkyk0ZcMXgSnMd
机械臂速成小指南(十三):轨迹规划概述https://blog.csdn.net/m0_53966219/article/details/125828466?fromshare=blogdetail&sharetype=blogdetail&sharerId=125828466&sharerefer=PC&sharesource=qq_52769953&sharefrom=from_link
机器人控制与轨迹规划https://blog.csdn.net/qq_37469992/article/details/112131666?fromshare=blogdetail&sharetype=blogdetail&sharerId=112131666&sharerefer=PC&sharesource=qq_52769953&sharefrom=from_link
【NUBUS五次非均匀B样条轨迹规划及机械臂仿真】 https://www.bilibili.com/video/BV1gX4y1u7gY/?share_source=copy_web&vd_source=4eaa4760820b4cda603e510d556578ac
【一起用Matlab从零手写六轴机械臂正逆解和轨迹规划】 https://www.bilibili.com/video/BV1UY411N7Xr/?share_source=copy_web&vd_source=4eaa4760820b4cda603e510d556578ac (不调用机器人工具箱)
六自由度机器人(机械臂)运动学建模及运动规划系列(四)——轨迹规划https://blog.csdn.net/weixin_47849087/article/details/126143953?fromshare=blogdetail&sharetype=blogdetail&sharerId=126143953&sharerefer=PC&sharesource=qq_52769953&sharefrom=from_link
机器人基础-机器人轨迹规划 https://yv6uc1awtjc.feishu.cn/wiki/Zmk2we1JQiv9gBkyk0ZcMXgSnMd
【适用所有机械臂!轨迹跟踪仿真!matlab算法!手把手教程|源码公开】 https://www.bilibili.com/video/BV12q4y1A7fi/?share_source=copy_web&vd_source=4eaa4760820b4cda603e510d556578ac
【《路径规划入门教程》——第一个专注于机械臂的路径规划课程】 https://www.bilibili.com/video/BV1G24y1M7ko/?share_source=copy_web&vd_source=4eaa4760820b4cda603e510d556578ac
再就是买的一些课程里涉及到的轨迹规划的章节
参考书籍:Principles of Robot Motion Theory,Algorithms,and Implementations. Planning Algorithms
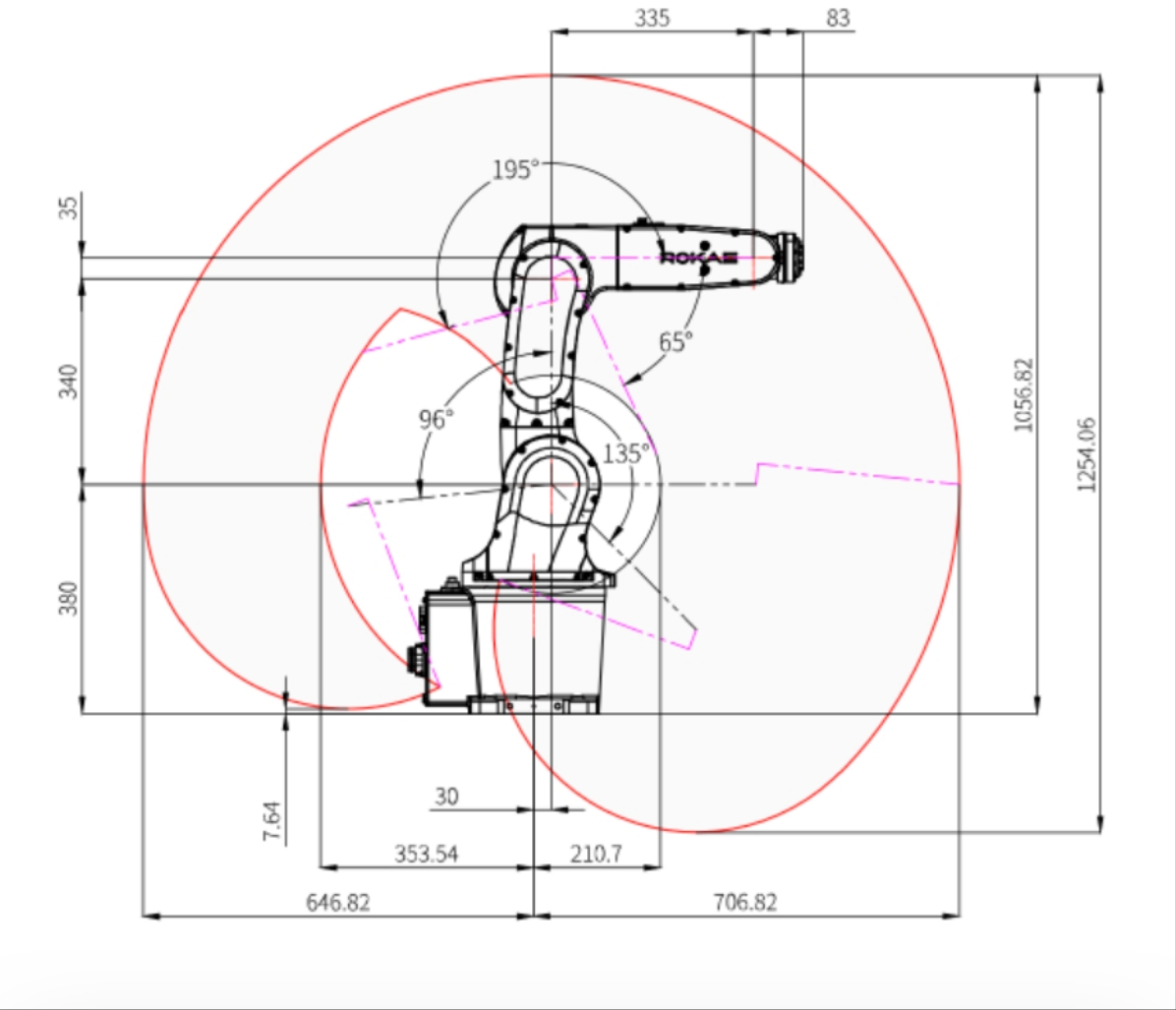
项目1:机械臂直线规划+梯形速度规划 任务要求 使用MATLAB软件对珞石XB7进行建模并实现直线规划+梯形速度规划。
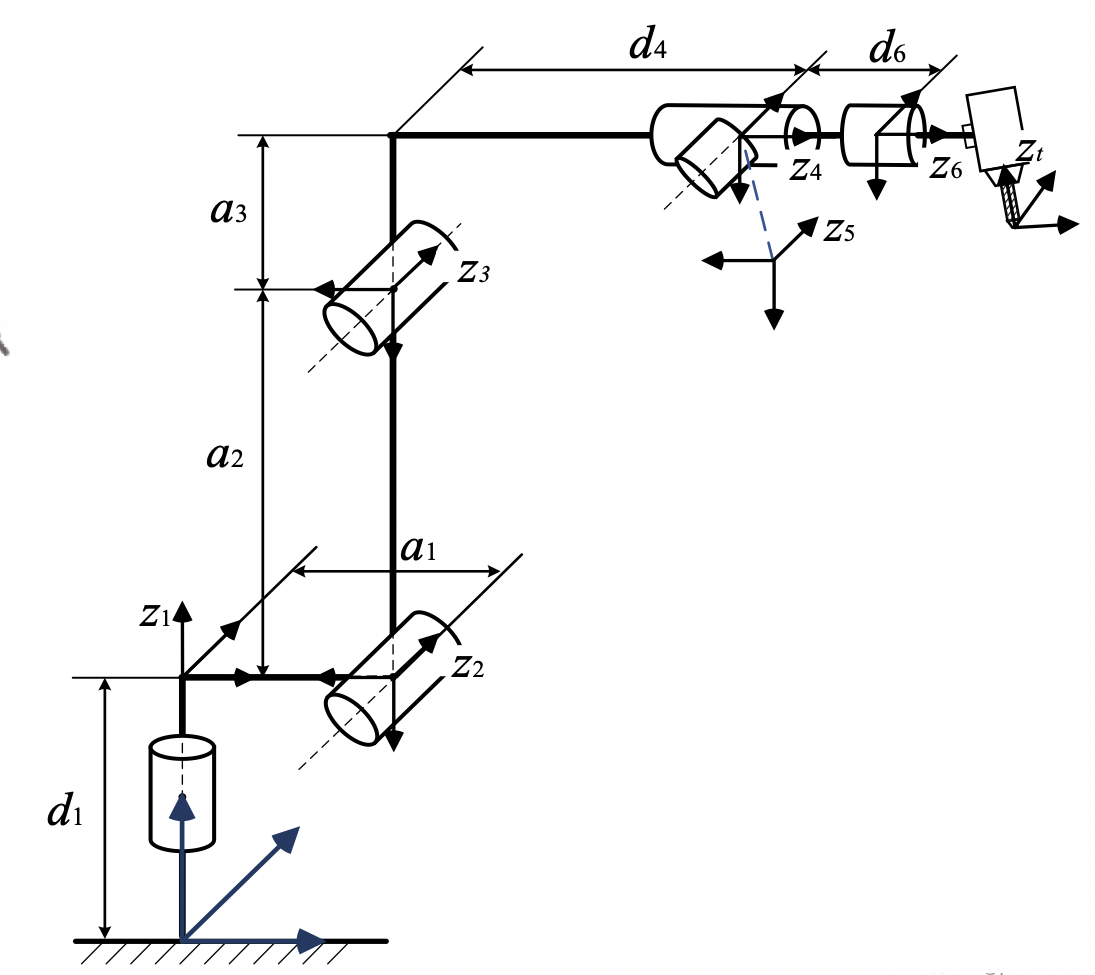
DH建模 D-H约定定义了一个机械臂的正向运动学方程,也就是从关节变量到末端执行器位置和姿态的映射,由上图可以得到DH各参数以及关节角限制。
建立机器人坐标系
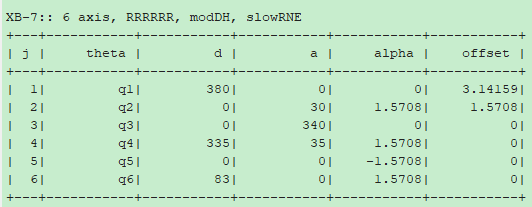
改进DH(MDH)建模
MATLAB对机器人DH建模 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 theta1 = 0 ; d1 = 380 ; a1 = 0 ; alpha1 = 0 ; theta2 = 0 ; d2 = 0 ; a2 = 30 ; alpha2 = pi /2 ; theta3 = 0 ; d3 = 0 ; a3 = 340 ; alpha3 = 0 ; theta4 = 0 ; d4 = 335 ; a4 = 35 ; alpha4 = pi /2 ; theta5 = 0 ; d5 = 0 ; a5 = 0 ; alpha5 = -pi /2 ; theta6 = 0 ; d6 = 83 ; a6 = 0 ; alpha6 = pi /2 ; L(1 ) = Link([theta1, d1, a1, alpha1], 'modified' ); L(2 ) = Link([theta2, d2, a2, alpha2], 'modified' );L(2 ).offset=-pi /2 ; L(3 ) = Link([theta3, d3, a3, alpha3], 'modified' ); L(4 ) = Link([theta4, d4, a4, alpha4], 'modified' ); L(5 ) = Link([theta5, d5, a5, alpha5], 'modified' ); L(6 ) = Link([theta6, d6, a6, alpha6], 'modified' ); L(1 ).qlim = [-170 *pi /180 , 170 *pi /180 ]; L(2 ).qlim = [-135 *pi /180 , 96 *pi /180 ]; L(3 ).qlim = [-45 *pi /180 , 187 *pi /180 ]; L(4 ).qlim = [-180 *pi /180 , 180 *pi /180 ]; L(5 ).qlim = [-68 *pi /180 , 68 *pi /180 ]; L(6 ).qlim = [-180 *pi /180 , 180 *pi /180 ]; robot = SerialLink(L, 'name' , '珞石XB-7' ); robot.display(); robot.teach();
直线轨迹规划+梯形速度规划 直线轨迹规划 ctraj函数用于生成两点之间的平滑轨迹。
ctraj的主要返回值是位姿轨迹,通常是一个4x4xN的矩阵,其中每个4x4切片表示一个齐次变换矩阵,描述机器人末端执行器在笛卡尔空间中该点的位姿(速度+方向),N是轨迹点的数量,由输入参数(如时间步长或插值点数)决定。
TC=ctraj(T0,T1,N),是一个从T0姿态到T1姿态的四维笛卡尔轨迹,其中有N个点沿着路径遵循梯形速度曲线。
TC=ctraj(T0,T1,S),S的各元素指定了沿路径的分段距离,这些值处于[0,1]范围内,第i个点对应于沿路径的距离s(i)。
1 2 3 4 5 6 7 8 9 10 11 12 13 T1=transl(-280 ,-300 , 450 ); T2=transl(-280 ,300 , 450 ); N = 50 ; Tc = ctraj(T1,T2,N); q=robot.ikine(Tc); plot3 (squeeze (Tc(1 ,4 ,:)),squeeze (Tc(2 ,4 ,:)),squeeze (Tc(3 ,4 ,:)));title('直线轨迹' ); robot.plot (q);
梯形速度规划
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 function [t, s] = trapezoid_vel_profile (dist, v_max, a_max) if v_max <= 0 || a_max <= 0 error('速度和加速度必须为正数' ); end if dist <= 0 t = 0 ; s = 0 ; return ; end t_acc = v_max / a_max; s_acc = 0.5 * a_max * t_acc^2 ; if 2 *s_acc > dist t_acc = sqrt (dist / a_max); t_total = 2 *t_acc; t_const = 0 ; s_const = 0 ; else s_const = dist - 2 *s_acc; t_const = s_const / v_max; t_total = 2 *t_acc + t_const; end t = linspace (0 , t_total, round (t_total/0.01 ))'; s = zeros (size (t)); for i = 1 :length (t) if t(i ) <= t_acc s(i ) = 0.5 * a_max * t(i )^2 ; elseif t(i ) <= t_acc + t_const s(i ) = s_acc + v_max*(t(i )-t_acc); else t_dec = t(i ) - t_acc - t_const; s(i ) = (s_acc + s_const) + v_max*t_dec - 0.5 *a_max*t_dec^2 ; end end s = min (max (s/dist, 0 ), 1 ); end
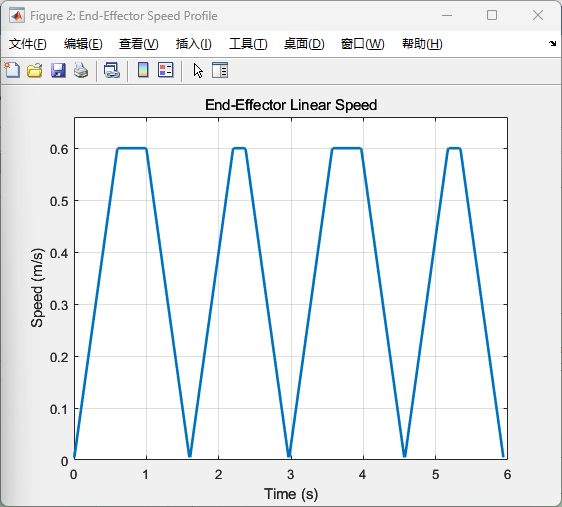
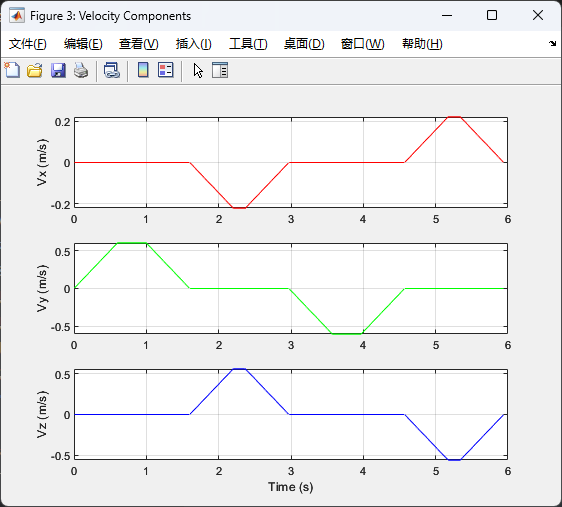
画矩形案例 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 theta1 = 0 ; d1 = 380 ; a1 = 0 ; alpha1 = 0 ; theta2 = 0 ; d2 = 0 ; a2 = 30 ; alpha2 = pi /2 ; theta3 = 0 ; d3 = 0 ; a3 = 340 ; alpha3 = 0 ; theta4 = 0 ; d4 = 335 ; a4 = 35 ; alpha4 = pi /2 ; theta5 = 0 ; d5 = 0 ; a5 = 0 ; alpha5 = -pi /2 ; theta6 = 0 ; d6 = 83 ; a6 = 0 ; alpha6 = pi /2 ; L(1 ) = Link([theta1, d1, a1, alpha1], 'modified' );L(1 ).offset=pi ; L(2 ) = Link([theta2, d2, a2, alpha2], 'modified' );L(2 ).offset=pi /2 ; L(3 ) = Link([theta3, d3, a3, alpha3], 'modified' ); L(4 ) = Link([theta4, d4, a4, alpha4], 'modified' ); L(5 ) = Link([theta5, d5, a5, alpha5], 'modified' ); L(6 ) = Link([theta6, d6, a6, alpha6], 'modified' ); robot = SerialLink(L, 'name' , 'XB-7' ); robot.display(); robot.teach(); scale = 0.001 ; v_max = 0.2 ; a_max = 0.2 ; T_1 = transl(-280 ,-300 , 450 ); T_2 = transl(-280 ,300 , 450 ); T_3 = transl(-450 ,300 , 880 ); T_4 = transl(-450 ,-300 , 880 ); T_5 = transl(-280 ,-300 , 450 ); delta_pos1 = norm(T_2(1 :3 ,4 ) - T_1(1 :3 ,4 )) * scale; delta_pos2 = norm(T_3(1 :3 ,4 ) - T_2(1 :3 ,4 )) * scale; delta_pos3 = norm(T_4(1 :3 ,4 ) - T_3(1 :3 ,4 )) * scale; delta_pos4 = norm(T_5(1 :3 ,4 ) - T_4(1 :3 ,4 )) * scale; [t_1, s_1] = trapezoid_vel_profile(delta_pos1, v_max, a_max); [t_2, s_2] = trapezoid_vel_profile(delta_pos2, v_max, a_max); [t_3, s_3] = trapezoid_vel_profile(delta_pos3, v_max, a_max); [t_4, s_4] = trapezoid_vel_profile(delta_pos4, v_max, a_max); Ts1 = ctraj(T_1, T_2, s_1); Ts2 = ctraj(T_2, T_3, s_2); Ts3 = ctraj(T_3, T_4, s_3); Ts4 = ctraj(T_4, T_5, s_4); q1 = robot.ikine(Ts1,'mask' , [1 1 1 1 1 1 ],'qlim' , true ); q2 = robot.ikine(Ts2,'mask' , [1 1 1 1 1 1 ],'qlim' , true ); q3 = robot.ikine(Ts3,'mask' , [1 1 1 1 1 1 ],'qlim' , true ); q4 = robot.ikine(Ts4,'mask' , [1 1 1 1 1 1 ],'qlim' , true ); q_total=[q1;q2;q3;q4]; x=squeeze (Ts1(1 ,4 ,:)); y=squeeze (Ts1(2 ,4 ,:)); z=squeeze (Ts1(3 ,4 ,:)); x1=squeeze (Ts2(1 ,4 ,:)); y1=squeeze (Ts2(2 ,4 ,:)); z1=squeeze (Ts2(3 ,4 ,:)); x2=squeeze (Ts3(1 ,4 ,:)); y2=squeeze (Ts3(2 ,4 ,:)); z2=squeeze (Ts3(3 ,4 ,:)); x3=squeeze (Ts4(1 ,4 ,:)); y3=squeeze (Ts4(2 ,4 ,:)); z3=squeeze (Ts4(3 ,4 ,:)); x_all=[x;x1;x2;x3];y_all=[y;y1;y2;y3];z_all=[z;z1;z2;z3]; plot3 (x_all,y_all,z_all);robot.plot (q_total, 'fps' , 100 , 'trail' , {'r' ,'LineWidth' ,2 }, 'nobase' , 'notiles' ); current_time = 0 ; t1 = t_1 + current_time; current_time = current_time + t_1(end ); t2 = t_2 + current_time; current_time = current_time + t_2(end ); t3 = t_3 + current_time; current_time = current_time + t_3(end ); t4 = t_4 + current_time; t_total = [t1; t2; t3; t4]; dx = diff(x_all) * scale; dy = diff(y_all) * scale; dz = diff(z_all) * scale; dt = diff(t_total); vx = dx ./ dt; vy = dy ./ dt; vz = dz ./ dt; speed = sqrt (vx.^2 + vy.^2 + vz.^2 ); time_mid = t_total(1 :end -1 ) + dt/2 ; figure ('Name' ,'End-Effector Speed Profile' );plot (time_mid, speed, 'LineWidth' , 2 );xlabel('Time (s)' ); ylabel('Speed (m/s)' ); title('End-Effector Linear Speed' ); grid on; ylim([0 v_max*1.1 ]); figure ('Name' ,'Velocity Components' )subplot(3 ,1 ,1 ); plot (time_mid, vx, 'r' );ylabel('Vx (m/s)' ); grid on; subplot(3 ,1 ,2 ); plot (time_mid, vy, 'g' );ylabel('Vy (m/s)' ); grid on; subplot(3 ,1 ,3 ); plot (time_mid, vz, 'b' ); ylabel('Vz (m/s)' ); xlabel('Time (s)' ); grid on; function [t, s] = trapezoid_vel_profile (dist, v_max, a_max) if v_max <= 0 || a_max <= 0 error('速度和加速度必须为正数' ); end if dist <= 0 t = 0 ; s = 0 ; return ; end t_acc = v_max / a_max; s_acc = 0.5 * a_max * t_acc^2 ; if 2 *s_acc > dist t_acc = sqrt (dist / a_max); t_total = 2 *t_acc; t_const = 0 ; s_const = 0 ; else s_const = dist - 2 *s_acc; t_const = s_const / v_max; t_total = 2 *t_acc + t_const; end t = linspace (0 , t_total, round (t_total/0.01 ))'; s = zeros (size (t)); for i = 1 :length (t) if t(i ) <= t_acc s(i ) = 0.5 * a_max * t(i )^2 ; elseif t(i ) <= t_acc + t_const s(i ) = s_acc + v_max*(t(i )-t_acc); else t_dec = t(i ) - t_acc - t_const; s(i ) = (s_acc + s_const) + v_max*t_dec - 0.5 *a_max*t_dec^2 ; end end s = min (max (s/dist, 0 ), 1 ); end
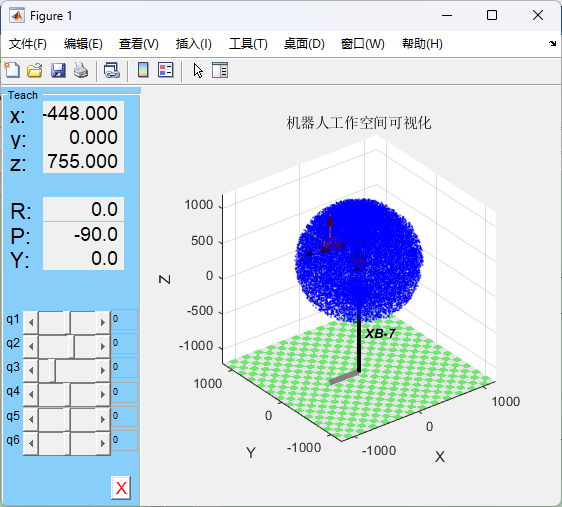
工作空间可视化
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 theta1 = 0 ; d1 = 380 ; a1 = 0 ; alpha1 = 0 ; theta2 = 0 ; d2 = 0 ; a2 = 30 ; alpha2 = pi /2 ; theta3 = 0 ; d3 = 0 ; a3 = 340 ; alpha3 = 0 ; theta4 = 0 ; d4 = 335 ; a4 = 35 ; alpha4 = pi /2 ; theta5 = 0 ; d5 = 0 ; a5 = 0 ; alpha5 = -pi /2 ; theta6 = 0 ; d6 = 83 ; a6 = 0 ; alpha6 = pi /2 ; L(1 ) = Link([theta1, d1, a1, alpha1], 'modified' );L(1 ).offset=pi ; L(2 ) = Link([theta2, d2, a2, alpha2], 'modified' );L(2 ).offset=pi /2 ; L(3 ) = Link([theta3, d3, a3, alpha3], 'modified' ); L(4 ) = Link([theta4, d4, a4, alpha4], 'modified' ); L(5 ) = Link([theta5, d5, a5, alpha5], 'modified' ); L(6 ) = Link([theta6, d6, a6, alpha6], 'modified' ); L(1 ).qlim = [-170 *pi /180 , 170 *pi /180 ]; L(2 ).qlim = [-135 *pi /180 , 96 *pi /180 ]; L(3 ).qlim = [-45 *pi /180 , 187 *pi /180 ]; L(4 ).qlim = [-180 *pi /180 , 180 *pi /180 ]; L(5 ).qlim = [-68 *pi /180 , 68 *pi /180 ]; L(6 ).qlim = [-180 *pi /180 , 180 *pi /180 ]; robot = SerialLink(L, 'name' , 'XB-7' ); robot.display(); num=30000 ; P=zeros (num,3 ); for i =1 :num q1=L(1 ).qlim(1 )+rand *(L(1 ).qlim(2 )-L(1 ).qlim(1 )); q2=L(2 ).qlim(1 )+rand *(L(2 ).qlim(2 )-L(2 ).qlim(1 )); q3=L(3 ).qlim(1 )+rand *(L(3 ).qlim(2 )-L(3 ).qlim(1 )); q4=L(4 ).qlim(1 )+rand *(L(4 ).qlim(2 )-L(4 ).qlim(1 )); q5=L(5 ).qlim(1 )+rand *(L(5 ).qlim(2 )-L(5 ).qlim(1 )); q6=L(6 ).qlim(1 )+rand *(L(6 ).qlim(2 )-L(6 ).qlim(1 )); q=[q1 q2 q3 q4 q5 q6]; T=robot.fkine(q); P(i , :)=transl(T); end plot3 (P(:,1 ),P(:,2 ),P(:,3 ), 'b.' , 'markersize' ,1 );xlabel('X (mm)' ); ylabel('Y (mm)' ); zlabel('Z (mm)' ); title('机器人工作空间可视化' ); axis equal; grid on robot.teach();
附录:MATLAB常用函数 位姿描述 齐次变换矩阵,是一个包括姿态和位置信息的4x4矩阵。每个T都看成转动+移动,只有移动则转动对应部分为单位向量,只有转动则移动部分对应向量为0。
transl(translation) transl函数用于创建一个表示平移的仿射变换矩阵
1 2 3 4 5 6 7 8 9 10 transl( [x, y, z] ); eg: T1=transl(-100 ,-100 ,300 ); display(T1); ->T1 = 1 0 0 -100 0 1 0 -100 0 0 1 300 0 0 0 1
trotx,troty,trotz trotx用于创建一个表示绕 x 轴旋转的仿射变换矩阵
1 2 3 4 5 6 7 8 9 10 11 12 trotx(theta), troty(theta), trotz(theta); eg: T1=trotx(180 ); display(T1); ->T1 = 1 0 0 0 0 -1 0 0 0 0 -1 0 0 0 0 1
移动+转动
1 2 3 4 5 6 7 8 9 10 eg: T1=transl(-100 ,-100 ,300 )*trotx(180 ); display(T1); T1 = 1 0 0 -100 0 -1 0 -100 0 0 -1 300 0 0 0 1
eul2r 欧拉角,绕自身坐标系旋转,右乘。
x为横滚,y为俯仰,z为偏航
rpy2r
运动学 建立机器人模型 Link Link类函数,基于DH法建模,建立其相关关系,DH法建模分改进型和标准型,Link类函数的一种用法是 R = Link([theta,d,a, alpha]),其中参数theta代表DH建模的关节角、参数d代表DH建模的连杆偏距、参数a代表DH建模的连杆长度、参数alpha代表DH建模的连杆转角。例如:L(1)=Link([1,2,3,4],‘modified’),其中modified表示用改进型DH法建模
1 2 3 4 5 6 7 8 9 10 11 12 13 14 theta1 = 0 ; d1 = 380 ; a1 = 0 ; alpha1 = 0 ; theta2 = 0 ; d2 = 0 ; a2 = 30 ; alpha2 = -pi /2 ; theta3 = 0 ; d3 = 0 ; a3 = 340 ; alpha3 = 0 ; theta4 = 0 ; d4 = 335 ; a4 = 35 ; alpha4 = -pi /2 ; theta5 = 0 ; d5 = 0 ; a5 = 0 ; alpha5 = pi /2 ; theta6 = 0 ; d6 = 83 ; a6 = 0 ; alpha6 = -pi /2 ; L(1 ) = Link([theta1, d1, a1, alpha1], 'modified' );L(1 ).offset=pi ; L(2 ) = Link([theta2, d2, a2, alpha2], 'modified' );L(2 ).offset=pi /2 ; L(3 ) = Link([theta3, d3, a3, alpha3], 'modified' ); L(4 ) = Link([theta4, d4, a4, alpha4], 'modified' ); L(5 ) = Link([theta5, d5, a5, alpha5], 'modified' ); L(6 ) = Link([theta6, d6, a6, alpha6], 'modified' );
关节角限制:
SerialLink 一个表示串联机械臂机器人的具体类,其中每个连杆和关节都通过使用DH参数的Link类对象进行描述。
通过在MATLAB命令行串口输出’doc SerialLink’可查看其详细内容。
以下是其常见的一些函数:
1.teach示教
2.plot
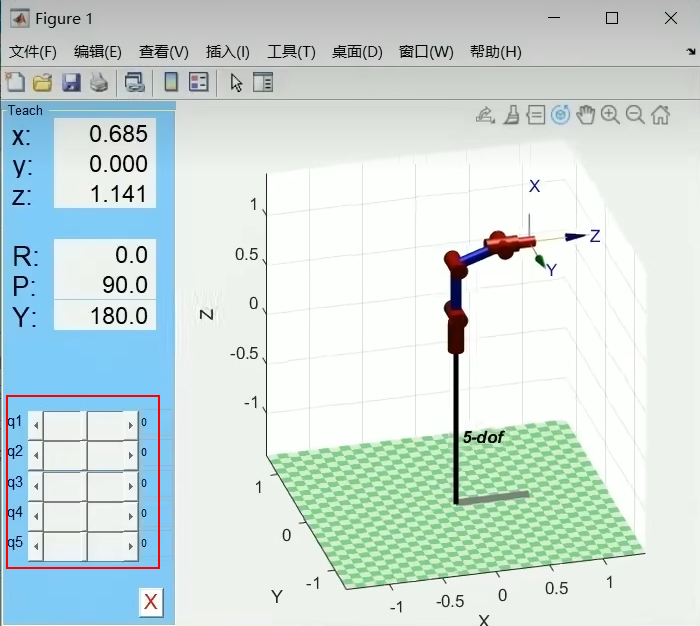
3.plot3d 三维模型展示(需导入STL文件)
只能用于标准型的DH参数建模。
1 2 mdl_puma560; p560.plot3d(qz,'view' ,[0 ,0 ]);
绝对路径
1 2 3 4 5 6 7 8 9 10 11 12 L(i ) = Link( [theta, d, a, alpha, sigma],'modified' ) L(i ).qlim = [ min , max ] Six_link = SerialLink( L, 'name' , 'Sixlink' ) Six_link.plot ( [theta_1, theta_2, ..., theta_n] ) Six_link.display Six_link.teach
运动学 fkine正向运动学 接受关节角度作为输入参数,并返回对应的末端执行器位置和姿态矩阵。
ikine逆向运动学 接受末端执行器位置和姿态矩阵作为输入参数,并返回对应的关节角度。
1 q1=Five_dof.ikine(T,'mask' ,[1 1 1 1 1 0 ]);//当用于欠自由度(小于6 )时,需用mask
ikine用于求数值解,不考虑关节限制
ikine6s用于求6轴机械臂的解析解
1 q2=Five_dof.ikunc(T);//当用于欠自由度(小于6 )时,不需用mask
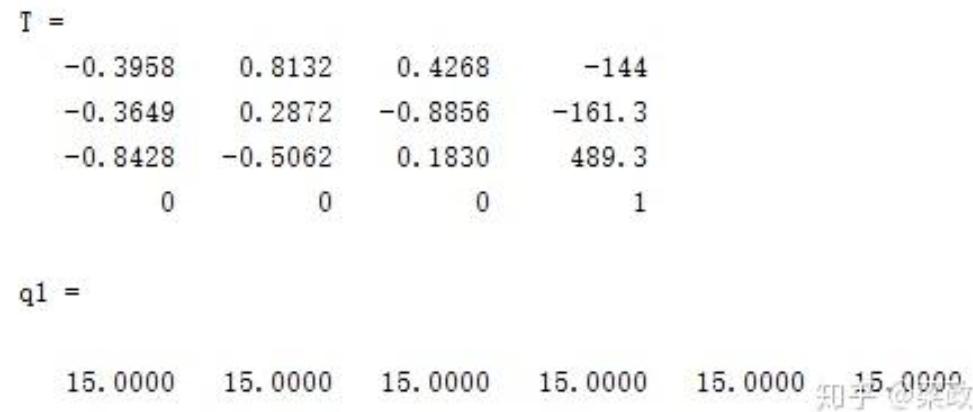
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 close all; L(1 )=Link('d' ,105.03 ,'a' ,0 ,'alpha' ,pi /2 ,'standard' ); L(2 )=Link('d' ,0 ,'a' ,-174.42 ,'alpha' ,0 ,'offset' ,-pi /2 ,'standard' ); L(3 )=Link('d' ,0 ,'a' ,-174.42 ,'alpha' ,0 ,'standard' ); L(4 )=Link('d' ,75.66 ,'a' ,0 ,'alpha' ,pi /2 ,'offset' ,-pi /2 ,'standard' ); L(5 )=Link('d' ,80.09 ,'a' ,0 ,'alpha' ,-pi /2 ,'standard' ); L(6 )=Link('d' ,44.36 ,'a' ,0 ,'alpha' ,0 ,'standard' ); robot=SerialLink(L(1 :6 ),'name' ,'Gluon_6L3' , 'manufacturer' ,'innfos' ) Theta=15 *ones (1 ,6 ); Theta=Theta/180 *pi ; T=robot.fkine(Theta) q1=robot.ikine(T)*180 /pi
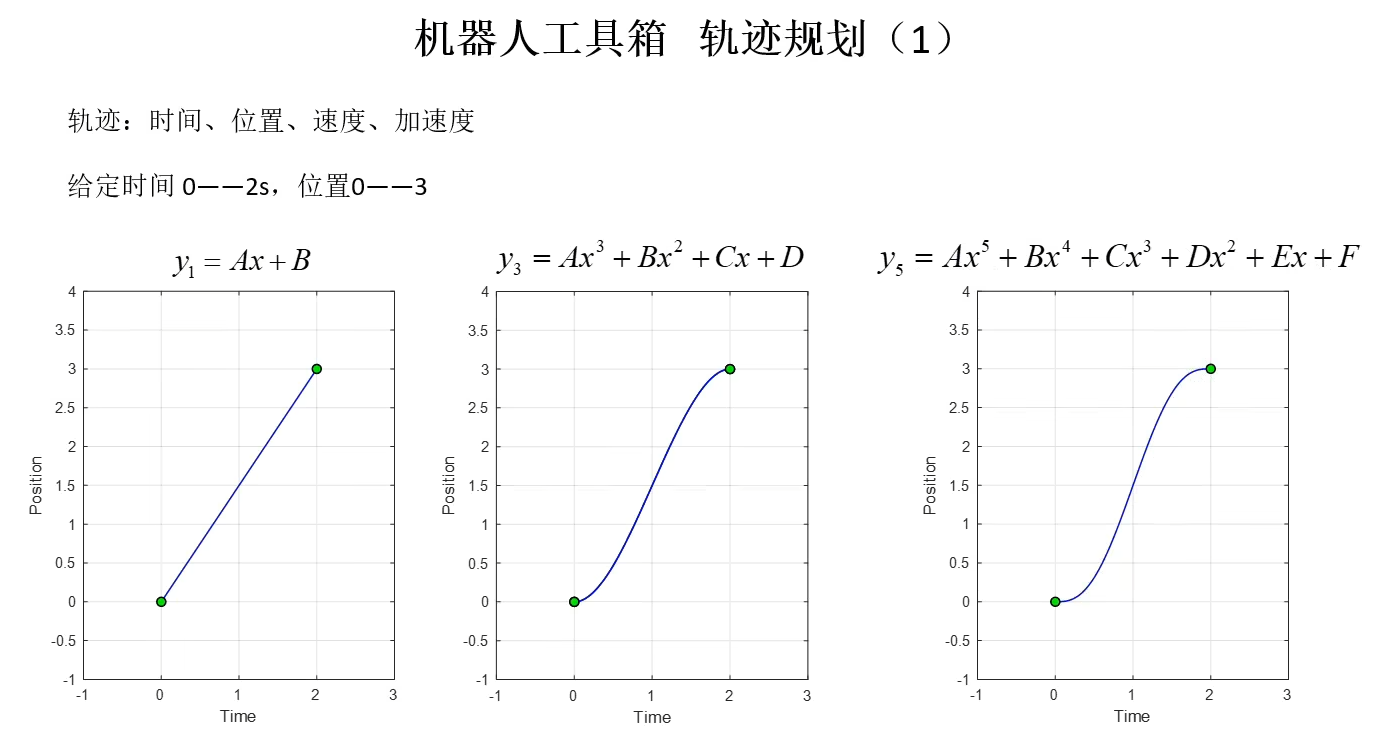
轨迹规划 一次多项式:首末速度突变,加速度为无穷大;
三次多项式:首末速度为0,加速度有突变;
五次多项式:首末速度、加速度为0,无突变。
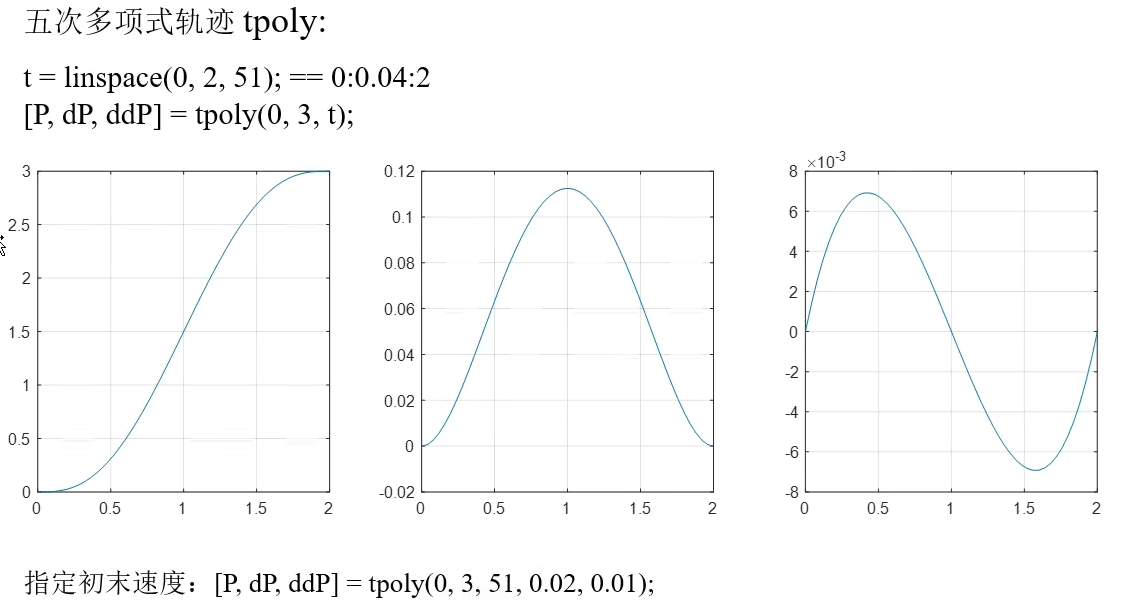
五次多项式轨迹tpoly 1 2 3 t=linspace (0 ,2 ,51 ) [P,dP,ddP]=tpoly(0 ,3 ,t); 指定初末速度:[P,dP,ddP]=tpoly(0 ,3 ,t,0.02 ,0.01 )
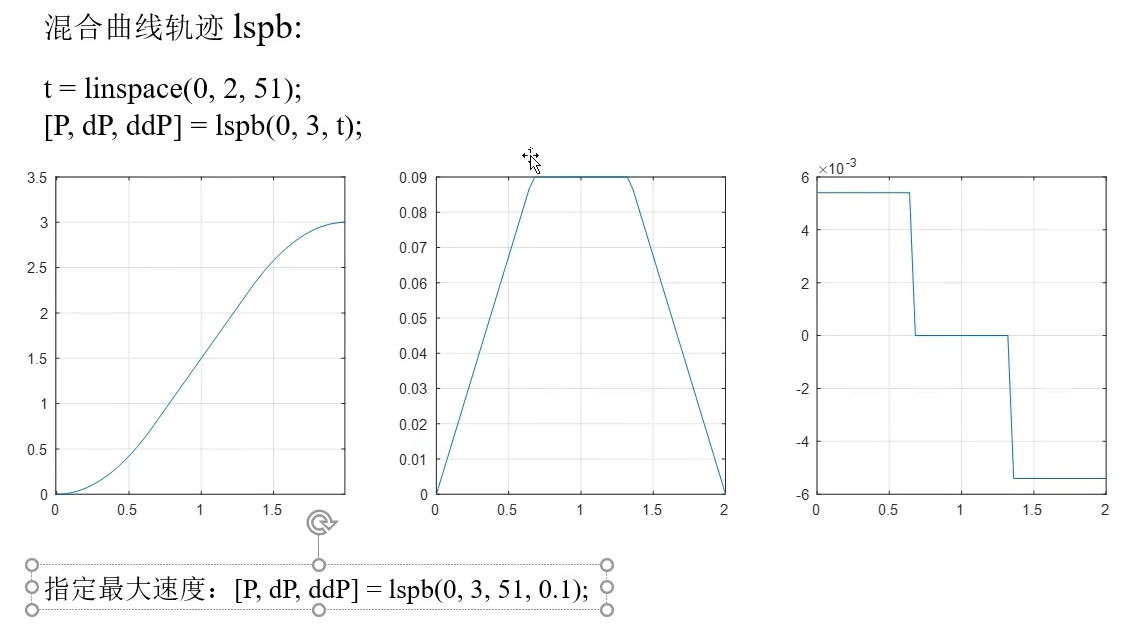
混合曲线轨迹lspb 看起来感觉和梯形速度规划差不多。
1 2 t=linspace (0 ,2 ,51 ); [p,dP,ddP]=lspb(0 ,3 ,t);
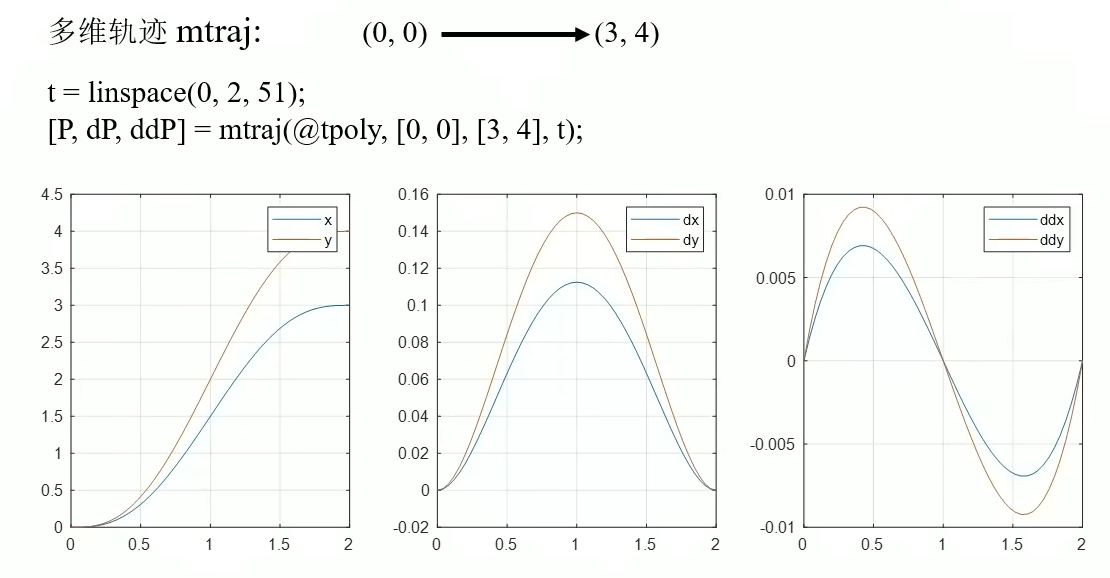
多维轨迹mtraj 1 2 t=linspace (0 ,2 ,51 ); [p,dP,ddP]=mtraj(@tpoly,[0 ,0 ],[3 ,4 ],t);
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 theta1 = 0 ; d1 = 380 ; a1 = 0 ; alpha1 = 0 ; theta2 = 0 ; d2 = 0 ; a2 = 30 ; alpha2 = pi /2 ; theta3 = 0 ; d3 = 0 ; a3 = 340 ; alpha3 = 0 ; theta4 = 0 ; d4 = 335 ; a4 = 35 ; alpha4 = pi /2 ; theta5 = 0 ; d5 = 0 ; a5 = 0 ; alpha5 = -pi /2 ; theta6 = 0 ; d6 = 83 ; a6 = 0 ; alpha6 = pi /2 ; L(1 ) = Link([theta1, d1, a1, alpha1], 'modified' );L(1 ).offset=pi ; L(2 ) = Link([theta2, d2, a2, alpha2], 'modified' );L(2 ).offset=pi /2 ; L(3 ) = Link([theta3, d3, a3, alpha3], 'modified' ); L(4 ) = Link([theta4, d4, a4, alpha4], 'modified' ); L(5 ) = Link([theta5, d5, a5, alpha5], 'modified' ); L(6 ) = Link([theta6, d6, a6, alpha6], 'modified' ); L(1 ).qlim = [-170 *pi /180 , 170 *pi /180 ]; L(2 ).qlim = [-135 *pi /180 , 96 *pi /180 ]; L(3 ).qlim = [-45 *pi /180 , 187 *pi /180 ]; L(4 ).qlim = [-180 *pi /180 , 180 *pi /180 ]; L(5 ).qlim = [-68 *pi /180 , 68 *pi /180 ]; L(6 ).qlim = [-180 *pi /180 , 180 *pi /180 ]; robot = SerialLink(L, 'name' , 'XB-7' ); robot.display(); P1=[-280 ,-300 , 450 ]; P2=[-280 ,300 , 450 ]; t=linspace (0 ,2 ,51 ); Traj=mtraj(@tpoly,P1,P2,t); n=size (Traj,1 ); T=zeros (4 ,4 ,n); for i =1 :n T(:,:,i )=transl(Traj(i , :))*trotx(180 ); end Qtraj=robot.ikunc(T); robot.plot (Qtraj,'movie' ,'trail.gif' ,'trail' , {'r' ,'LineWidth' ,2 });
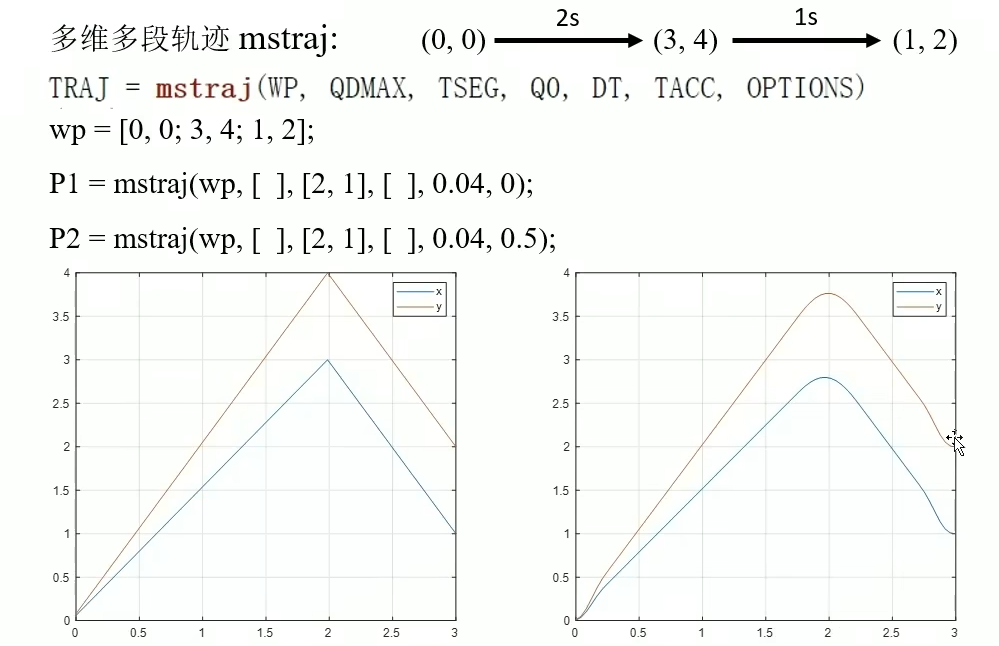
多维多段轨迹mstraj
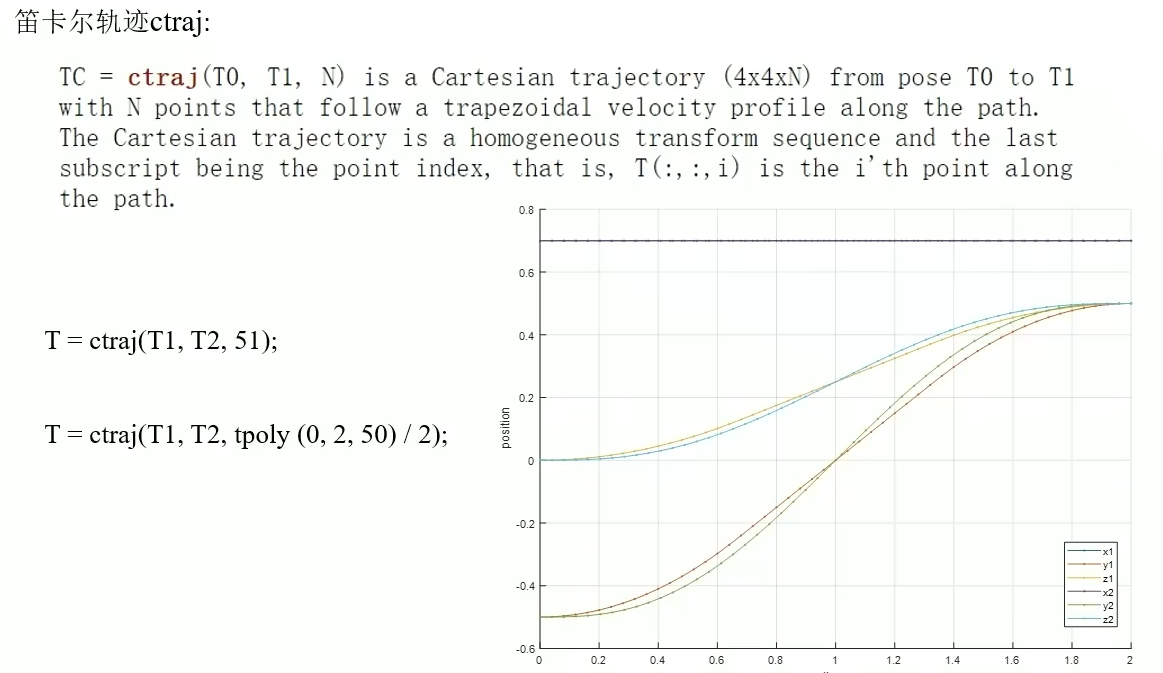
笛卡尔轨迹ctraj
参考资源 【台大机器人学之运动学——林沛群(含课件+书籍)】 https://www.bilibili.com/video/BV1v4411H7ez/?share_source=copy_web&vd_source=4eaa4760820b4cda603e510d556578ac
MATLAB机器人工具箱10.4 机械臂仿真教学https://www.bilibili.com/video/BV1q44y1x7WC?spm_id_from=333.788.videopod.episodes&vd_source=a9d487fcf1a579639c6348eb5a9321db&p=4
CSDN:工业六轴机器人常见的STD(标准)-DH模型建立方法https://blog.csdn.net/Vittore_Li/article/details/121966473?fromshare=blogdetail&sharetype=blogdetail&sharerId=121966473&sharerefer=PC&sharesource=qq_52769953&sharefrom=from_link
详细介绍如何使用MATLAB中的机器人工具箱建立机器人模型(DH法建模)(机械臂)https://blog.csdn.net/qq_44339029/article/details/109708454?fromshare=blogdetail&sharetype=blogdetail&sharerId=109708454&sharerefer=PC&sharesource=qq_52769953&sharefrom=from_link
黄磊.工业机器人笛卡尔空间轨迹规划算法研究与应用[D].电子科技大学,2024.DOI:10.27005/d.cnki.gdzku.2024.004056.
CSDN:【Matlab 六自由度机器人】系列文章汇总https://blog.csdn.net/AlbertDS/article/details/123968265?fromshare=blogdetail&sharetype=blogdetail&sharerId=123968265&sharerefer=PC&sharesource=qq_52769953&sharefrom=from_link
知乎:机器人工程师进阶之路https://www.zhihu.com/column/c_1241771327444774912
知乎:机器人技术基础之运动学https://www.zhihu.com/column/c_1693921850789429248?utm_campaign=&utm_medium=social&utm_psn=1896366318900467549&utm_source=qq